This is a topic that lends itself well to ray-tracing. It is the photons that we seek to simulate, which is exactly what a ray-tracing algorithm does in the visualization process. We wish to consider both the linear and angular momentum contributions in our visualization, and thirdly the gravitational contributions. So the first step is to generate simulations of Special Relativistic (SR) phenomena - both linear relativistic velocities, and relativistic rotational (spin) velocities. While the linear acceleration of the rotating object's surface implies a General Relativistic (GR) solution, an SR visualization may serve. A GR visualization introduces gravitational spacetime warping, which may or may not be relevant at the particle level, as we shall most surely see.

Analyzing relativistic orbits and spins leads to a couple of interesting conclusions. The first is Thomas Precession (PDF), the phenomenon that explains the electron's anomalous spin magnetic moment.

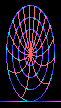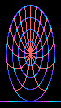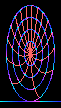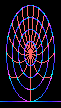
Figure 1

The example [1] of rigid-disk visualization (the cartwheel in Figure 1) shows a redistribution of the surface features of the rotating rim. Such redistribution suggests that potential may be redistributed about the rim. Extrapolating the redistribution of area to a spinning sphere suggests a similar redistribution of area between the slow moving poles and the rapidly moving equator. Again, such redistribution suggests a similar redistribution of potential about the surface, leading directly to the redistribution of accompanying forces.

In the following four images[2], and accompanying animations, we observe three tires from Mr. Tompkin's bicycle. George Gamov's Mr. Tompkins lives on a world where the speed of light is 30 km/h, so we needn't move very fast to experience relativistic effects. The Red Tire is stationary. The Green Tire's rim is spinning clockwise at 93% of the speed of light (0.93c). The Blue Tire is rolling along the ground, parallel to the other two tires, from left to right at 0.93c. The Camera position is critical, since any asymmetries have large effects. Click On the pictures to see the MPEG animations.

Front View: The Camera is between the Green and Red tires, and a little higher than the top rims. Blue is length contracted in the direction of motion. Blue's top rim is marginally closer than its bottom, so Blue appears tilted in the direction of motion. This MPEG file is 403KB.

Left View: The Camera is to the left of the Green Tire on a 45 degree diagonal. Blue racing away from us at 93% of lightspeed. Notes to myself: I am not yet convinced that this simulation is correct. Look for symmetries in the rolling and spinning wheels I would like to examine various contributions of Doppler due to rotation vs doppler due to motion vs contraction's contribution.

Right View: The Camera is to the right of the Red Tire on a 45 degree diagonal. Blue arrives close behind its own wavefront since it is moving towards us at 93% of its own light. Notes to myself: Again I am cautious about the credibility of this animation. Why is the Blue's angle different in the Left and Right Views? Where is the symmetry? This MPEG is 206KB

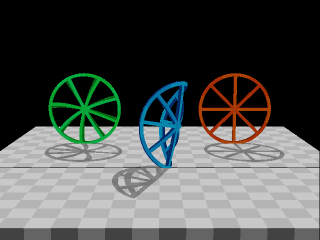Front Twister: This is the same view as Front View, with a twist. Blue is spinning about its own vertical axis and not rolling. Thus Blue appears to be warped. The analysis is left for you. This MPEG file is 386KB.

A General Relativistic visualization[3] is supplied to show the differences between SR and GR simulations. Shown is a rigidly rotating disk of dust, similar to our rotating cartwheels with one big difference. The dust cloud is sufficiently massive to distort Spacetime, causing light to orbit about the disk so that the multiple mirages of the backside can be seen. This MPEG file is 6.8MB. (Here is a bigger 15MB version.)

1. The Lorentz Contracted Cartwheel animation courtesy of Andrew Hamilton, from the Center for Astrophysics and Space Astronomy, U of Colo - Boulder.

2. The four bicycle tire Rolling Wheels animations (Rollende Räder) are courtesy of Corvin Zahn, of the Institute of Astronomy and Astrophysics, Tübingen.

3. General Relativity - rigidly rotating disk of dust, courtesy of Daniel Weiskopf of the Universität Stuttgart (University of Stuttgart) and Institute of Astronomy and Astrophysics, Tübingen

4. Additional rigid-disk or 'cartwheel', and other relativistic visualizations can be found in Germany at the Institute of Astronomy and Astrophysics, Tübingen